Вопросы и ответы
Для чего используется коэффициент Шарпа?
Коэффициент Шарпа используется для измерения доходности инвестиций с поправкой на риск. Он помогает инвесторам оценить, является ли избыточная доходность портфеля результатом мастерства или просто результатом принятия на себя большего риска. Коэффициент позволяет инвесторам сравнивать различные инвестиционные возможности и оценивать, оправдывает ли потенциальная прибыль связанные с ней риски.
Как интерпретировать коэффициент Шарпа?
Более высокий коэффициент Шарпа указывает на лучшие показатели с поправкой на риск. При сравнении аналогичных портфелей или инвестиционных стратегий более высокий коэффициент Шарпа говорит о том, что портфель принес более высокую прибыль на единицу риска
Однако при принятии инвестиционных решений важно учитывать и другие факторы, а не полагаться только на коэффициент Шарпа
Что такое хороший коэффициент Шарпа?
Не существует универсального определения «хорошего» коэффициента Шарпа, поскольку его интерпретация зависит от склонности инвестора к риску и конкретного инвестиционного контекста. Как правило, положительный коэффициент Шарпа указывает на то, что инвестиции принесли сверхдоходы, превышающие безрисковую ставку. Сравнение коэффициентов Шарпа различных инвестиций может помочь выявить те из них, которые имеют лучшую доходность с учетом риска.
Может ли коэффициент Шарпа быть отрицательным?
Да, коэффициент Шарпа может быть отрицательным. Отрицательный коэффициент Шарпа указывает на то, что инвестиции не оправдали безрисковую ставку или не компенсировали должным образом уровень принятого риска. Отрицательный коэффициент говорит о том, что доходность инвестиций не оправдала волатильность или риск.
Для всех ли типов инвестиций подходит коэффициент Шарпа?
Коэффициент Шарпа можно использовать для различных типов инвестиций, включая акции, облигации, взаимные фонды и портфели
Однако важно учитывать специфические характеристики и факторы риска, связанные с каждым типом инвестиций. Различные инвестиции могут иметь разные эталоны или безрисковые ставки, что может повлиять на интерпретацию их коэффициентов Шарпа
Может ли коэффициент Шарпа предсказать будущие результаты?
Коэффициент Шарпа основан на исторических данных и предполагает, что прошлые результаты свидетельствуют о будущих результатах
Однако важно отметить, что рыночные условия и инвестиционные стратегии могут меняться с течением времени. Поэтому, хотя коэффициент Шарпа дает представление об эффективности инвестиций с поправкой на риск, на него не следует полагаться как на предсказатель будущих доходов
Коэффициент альфа (α-коэффициент, coefficient alpha)
Коэффициент альфа показывает превышение среднего результата фонда над нормативным результатом, который рассчитывается в соответствии с полученным ранее коэффициентом бета.
Формула расчета альфа на отрезке в 3 года:
α = Y – (r + β * (IND – r)),
где r – средняя доходность безрискового актива (обычно за ставку безрискового актива принимают процентную ставку по депозитному вкладу);
IND – среднее значение прироста индекса за 36 месяцев, предшествующих дате расчета;
Y – среднее значение доходности фонда за 36 месяцев, предшествующих дате расчета.
Считается, что коэффициент альфа характеризует вклад управляющего фондом в итоговый результат. И предполагается, что исходя из этого следует искать ПИФы с высокой альфой. Ведь это те фонды, управляющие которых смогли показать результаты выше расчетных. Но тут есть свои нюансы.
- Необходимо, чтобы индекс для расчета альфы был подобран корректно, иначе расчет бесполезен.
- Отрицательное значение альфы может быть как следствием «некомпетентного управления», так и следствием высоких комиссий за управление. Рассмотрим данный нюанс на примере индексных фондов. В данном случае управляющие не занимаются выбором ценных бумаг, а просто копируют индекс, поэтому роль управляющего здесь сведена к минимуму, а альфа индексного фонда должна быть равна нулю. Но многие индексные фонды имеют отрицательную альфу, что связано с расходами ПИФа, которые в данном примере и выражает альфа.
- Наиболее важный нюанс заключается в том, что альфа не предоставляет аналитических данных. То есть по альфе невозможно понять, почему результат фонда превосходил расчетный. Что это было: искусство одного управляющего, налаженная система по управлению капиталом или просто везение?
Для того чтобы понять, какой же вклад внес управляющий в итоговый результат, мы используем систему MARQ — Measurement Arsagera Reallocation Quality. В отчете MARQ содержится детальная информация об эффективности совершенных в отчетном периоде перекладок из одних активов в другие, то есть информация о том, правильные ли решения принимал управляющий в отчетном периоде.
Виды инвестиционных портфелей
Основная цель портфельного инвестора – создать оптимальный баланс риска и доходности своих активов.
Рассмотрим следующие способы формирования инвестиционного портфеля.
По степени риска
Выделяют три типа инвестиционного портфеля.
Защитный
Формируется из активов с пониженным риском: банковские депозиты, ПИФы, недвижимость, высоконадежные облигации и акции крупнейших компаний с регулярными дивидендными выплатами.
Агрессивный
Портфель интересен тем, кто желает в кратчайшие сроки получить значительный доход. Отличительная черта данного типа портфеля – размещение более 50% всех средств в акции. Несмотря на то, что агрессивная стратегия может показать инвестору впечатляющую доходность, вероятность полной потери вложенных средств также значительно увеличивается.
Сбалансированный
Наиболее оптимальным вариантом инвестирования служит сбалансированная стратегия. Портфель следует формировать преимущественно из государственных и корпоративных облигаций с высоким кредитным рейтингом, акций крупнейших компаний, лишь незначительную часть средств направлять на покупку высокодоходных активов.
По методу управления активами
Основные методы управления финансовыми инструментами следующие:
- пассивное управление,
- активное управление.
Ключевые особенности пассивного инвестирования:
- не требуется постоянной вовлеченности к отслеживанию рыночных котировок;
- низкий уровень риска;
- потенциальная доходность ненамного превышает ставку по банковским депозитам.
Основной принцип управления – купить и держать.
Что касается активного управления, то данный метод сводится к постоянному отслеживанию рыночных тенденций и частому изменению структуры портфеля.
По способу получения прибыли
Выделяют два вида.
Портфель роста
Рекомендуется покупать акции, по которым прогнозируется значительный рост их котировок. Основной способ получения прибыли сводится к продаже акций в будущем по более дорогой цене.
Портфель дохода
Соответствующий портфель создается для получения регулярной прибыли
Инвестору необходимо обращать внимание на дивидендные акции и купонные облигации высоконадежных эмитентов
По срокам достижения целей
Бывают краткосрочный, среднесрочный и долгосрочный портфели.
Краткосрочный
Инвестиционный горизонт составляет 1–2 года.
Портфель формируется преимущественно из высоколиквидных активов, которые могут быть быстро проданы. Следует сконцентрироваться на дивидендных акциях крупнейших компаний и акциях роста, облигациях, валюте и банковском депозите.
Что касается облигаций, то их можно продать раньше даты погашения. Поэтому инвестор может включить в портфель как краткосрочные, так и долгосрочные облигации. По поводу эмитента облигаций необходимо сказать, что государственные облигации в приоритете, однако можно приобрести и корпоративные облигации. Единственное условие – облигация должна быть с низким уровнем риска.
Среднесрочный
Формируется на срок от 1 до 5 лет.
Среднесрочный портфель уже допускает возможность включать в себя рискованные инструменты с повышенным доходом, однако больше 50% активов должны быть всё же в виде надежных ценных бумаг с умеренной доходностью.
Добавить можно паи инвестиционных фондов и структурные ноты.
Долгосрочный
Формируется пассивным инвестором на срок от 5 лет. Подход к покупке активов основан на поиске перспективных компаний с прогнозируемым денежным потоком дивидендов. Инвестиционная привлекательность ценной бумаги – более важный фактор, нежели ее степень ликвидности.
Включить можно акции банков с госучастием, страховых компаний и металлургических концернов. Среди облигации можно рассмотреть рублевые облигации вышеназванных компаний, еврооблигации и долгосрочные государственные облигации.
Расчет коэффициента Шарпа
Многие инвесторы, любуясь на растущие цифры на счете, упускают факт повышения рисков портфеля. Коэффициент Шарпа показывает же достаточно полную картину эффективности портфеля и рассчитывается как отношение среднего дохода по сделкам к уровню риска. Более высокие результаты по коэффициенту говорят о более эффективном способе торговли. Кроме того, коэффициент Шарпа позволяет построить прогнозы относительно стабильности получения прибыли.
Формула для расчета коэффициента в стандартном виде следующая: (Rp-Rf)/стандартное отклонение от ожидаемой средней доходности, где Rp – это ожидаемая прибыль, а Rf – безрисковый доход. В расчёте под стандартным отклонением от ожидаемой средней доходности понимается риск.
Подводя итоги, розничные и институциональные инвесторы нуждаются в надлежащем методе количественной оценки прибыли по отношению к риску при выборе инвестиционного выбора.
Прогнозирование потенциальной доходности недостаточно при оценке жизнеспособности инвестиций в течение определенного периода времени.
Коэффициент Шарпа обеспечивает лучшее представление о привлекательности инвестиций благодаря включению риска в их расчет. Это позволяет инвесторам лучше понять доходность по отношению к риску, принимаемому при владении активом.
Однако, как и во всех отношениях, коэффициент Шарпа имеет свои недостатки. Он использует стандартное отклонение при условии, что доходы распределяются равномерно. В связи с этим некоторые трейдеры и инвесторы предпочитают использовать коэффициент Сортино, который при расчете использует только стандартное отклонение в сторону понижения.
Коэффициент Шарпа – расчет и примеры на Форекс и фондовом рынке
Начиная торговать на фондовом рынке или на рынке Форекс, стоит оценить разумность вложений в выбранную валютную пару или фьючерс. В этом вопросе так же поможет коэффициент Шарпа. Для наглядности давайте рассмотрим примеры.
Пример расчета коэффициента Шарпа
Для того, чтобы выбрать из двух стратегий, оценивать их эффективность будем при помощи коэффициента Шарпа.
Например, при торговле на рынке forex доходность первой стратегии составляет 8% при коэффициенте отклонения 5%. Есть еще одна стратегия с доходностью 6% и стандартным отклонением 2%. На первый взгляд, кажется, что первая стратегия привлекательнее, ведь доходность по ней выше на 2 %. Однако, рассчитав коэффициент Шарпа (КШ), видим следующее:
КШ первой стратегии=8/5=1,6 КШ второй стратегии=6/2=3 Таким образом, сравнив значения показателя Шарпа, видим, что вторая стратегия менее рискованная, хотя доходность немного ниже.
Существует много встроенных инструментов, в которых уже посчитаны основные коэффициенты. Давайте рассмотрим расчет Шарпа на реальном примере. Например, вы решили купить акции Сбербанка. Средняя волатильность акций составляет 2,4% в день при доходности 10,72% в месяц или 0,357% в день. Используя эти данные, подставим их в формулу и получим следующий результат:
КШ = 0,357%/2,4%=0,1485. Достаточно низкий коэффициент, что говорит о высоком риске инвестирования. Стоит отметить, что волатильность, то есть колебания цены, может быть ниже в долгосрочном периоде.
Стандартное отклонение
Расчет стандартного отклонения в торговом терминале производится автоматически. Данный показатель дает возможность определить, каким именно образом изменится (уменьшится или увеличится) доходность выбранного актива в сравнении со средней доходностью за выбранный временной промежуток.
Рассмотрим пример
Для наглядности можно оценить риск стратегий, сравнивая две различные выборки данных.
В первом случае прибыльность торговых сделок составила: 3, 2, 5, 0, 4 %. Среднее значение будет равно 2,8 %. Результат его вычитания из каждого показателя доходности равен: 0,2; -0,8; 2,2; -2,8; 1,2 %. При возведении каждого значения в квадрат нужно вычислить их сумму, затем найти среднее арифметическое и из полученного значения вычислить квадратный корень:
Sqrt((0,4 % + 0,64 % + 4,84 % + 7,84 % + 1,44 %) / 5) = 3,03 %
Во втором случае прибыльность торговых сделок составила: 2, 1, 0, 4, 6 %. Их среднее арифметическое равно 2,6%. Результаты аналогичной предыдущему способу операции: -0,6; -1,6; -2,6; 1,4; 3,4 %. Затем, как и в предыдущем случае:
Sqrt((0,36 % + 2,56 % + 6,76 % + 1,96 % + 11,56 %) / 5) = 4,64 %
Результат сравнения — первая стратегия менее рискованна, чем вторая, поскольку волатильность доходности у нее меньше.
Хотя коэффициент Шарпа представляет собой один из важных эталонов доходности с учетом риска, его следует использовать вместе с аналитической информацией.
Коэффициент Шарпа
Смысл коэффициента Шарпа (sharpe ratio) в сопоставлении доходности и риска – т.е. чем больше его значение, тем более высокая доходность может быть получена при определенном уровне риска. Математически sharpe ratio это разница между доходностью актива и доходностью безрисковой инвестиции, деленная на стандартное отклонение доходности актива:

Довольно интересным понятием является «доходность безрисковой инвестиции». Обычно под ней подразумевается банковский депозит (Сбербанк), однако в качестве бенчмарка может использоваться и средняя доходность крупного биржевого индекса (напр. S&P500 при торговле на американском рынке), либо ставка по государственным облигациям США.
Поэтому при сравнении коэффициентов Шарпа нужно обратить внимание на этот момент – банки могут брать доход безрисковой инвестиции, близкий к нулю, за счет чего получить очень высокие коэффициенты вплоть до сотен и тысяч. Идеальный коэффициент, стремящийся к бесконечности, получается у столь же идеальной кривой дохода, равномерно возрастающей по экспоненте и не имеющей крупных просадок
На практике хорошим значением считается примерно от 0.5 и выше.
Пример расчета коэффициента Шарпа
Допустим, наш инвестиционный портфель под управлением показал доходность 25%, причем стандартное отклонение составило 10%. За то же время депозит в Сбербанке дал нам 5%. В этом случае sharpe ratio будет равен (25-5)/10 = 2. Можно сказать, что на 1% риска было получено 2% прибыли сверх безрисковой (гарантированной) доходности.
При равной доходности меньшая величина стандартного отклонения (более гладкая и предпочтительная торговля) даст большее значение sharpe ratio. При торговле валютой коэффициент Шарпа часто рассчитывается в специальных системах мониторинга – например, у FXOpen или в myfxbook.
Что такое стандартное отклонение в системе? Представим, что у нас есть результаты некоторой совокупности сделок (или доходности портфеля за разные периоды):
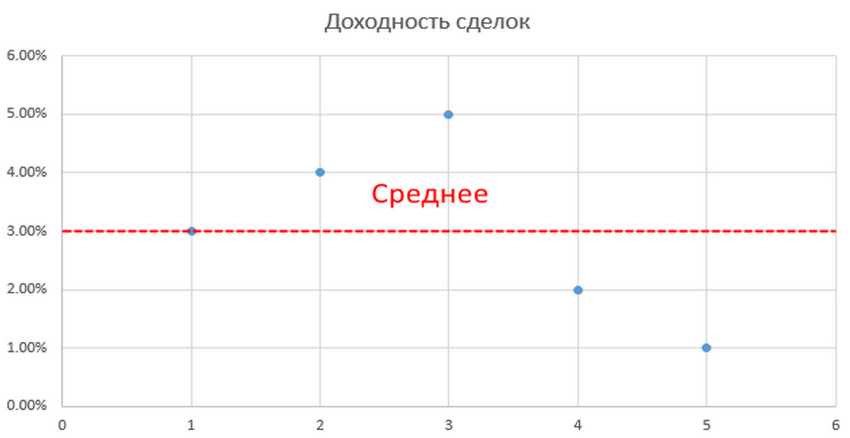
Тогда результат считается как

Недостатки коэффициента Шарпа:
-
Зависимость от рассматриваемого интервала и бенчмарка. Прошлая доходность не гарантирует будущей – поэтому показатель sharpe ratio подвержен изменениям, причем нередко довольно резким
- Любые колебания доходности (как положительные, так и отрицательные) в формуле для расчета коэффициента являются одинаково плохими – а значит, даже успешная торговля может дать низкие значения sharpe ratio
-
Нет различий между чередующимися и последовательными убытками, хотя на практике первый случай может означать слом торговой системы и уменьшение вероятности будущей прибыли
Тем не менее иногда коэффициент позволяет, особенно на периоде с прошедшим кризисом, сделать вывод о рисках торговли трейдера или фонда: при сравнении двух и более из них, показывающих равную доходность, наиболее предпочтительным будет тот, кто имеет более высокий коэффициент.
Как использовать коэффициент Шарпа для принятия инвестиционных решений
Коэффициент Шарпа измеряет отношение доходности инвестиционного портфеля к его риску. Понимание и использование этого показателя может быть полезно для инвесторов при принятии решений о распределении своих инвестиций.
Для использования коэффициента Шарпа в инвестиционных решениях следует учесть следующие аспекты:
- Оцените доходность портфеля: Рассчитайте доходность вашего инвестиционного портфеля за определенный период времени. Доходность может быть выражена в процентах или абсолютной величине.
- Оцените риск портфеля: Оцените величину риска вашего портфеля, используя стандартное отклонение. Стандартное отклонение измеряет величину изменений цен активов в портфеле.
- Вычислите коэффициент Шарпа: Вычислите коэффициент Шарпа, разделив доходность портфеля на его риск. Чем выше коэффициент Шарпа, тем лучше соотношение доходности и риска.
- Сравните с другими портфелями или индексами: Сравните коэффициент Шарпа вашего портфеля с коэффициентами других портфелей или индексов. Это поможет вам сравнить эффективность вашего портфеля относительно других инвестиционных возможностей.
- Учтите индивидуальные потребности и цели: Инвестиционные решения должны быть приняты, исходя из ваших индивидуальных целей, срока инвестирования и уровня комфорта с риском.
- Проверьте результаты и внесите коррективы: Регулярно проверяйте результаты вашего портфеля и корректируйте его состав при необходимости. Изменение инвестиционной стратегии может быть оправдано на основе анализа коэффициента Шарпа.
Использование коэффициента Шарпа для принятия инвестиционных решений поможет вам оценить соотношение между доходностью и риском в вашем портфеле. Он может быть полезным инструментом для выбора наиболее эффективных инвестиций и определения стратегии, которая соответствует вашим потребностям и целям.
Смотреть на коэффициент Шарпа отдельных инструментов нет смысла
Составляя портфель из двух разных инструментов с определенным коэффициентом Шарпа, итоговый портфель не будет
иметь средневзвешенный коэффициент Шарпа двух активов. А все дело в корреляции. Для примера возьмем два фонда со следующими характеристиками (см. таблицу 1).
Таблица 1. Сравнение коэффициента Шарпа двух отдельных активов и портфеля из них
| Доходность сверх безрисковой ставки | Волатильность | Коэффициент Шарпа | |
| Актив А | 12% | 10% | 1,2 |
| Актив Б | 10% | 10% | 1,0 |
| Общий портфель (корреляция активов — 0,5) | 11% | 8,7% | 1,27 |
Как видно, Шарп для итогового портфеля выше, чем у двух активов отдельно.
Анализ эффективности, критерии оценки
Существуют пять ключевых показателей для оценки эффективности инвестиционного портфеля.
Среднегодовая доходность
Показывает темп прироста стоимости активов за один финансовый год по отношению к размеру первоначальных инвестиций.
Стандартное отклонение
Данный критерий показывает степень рискованности портфеля. Чем выше стандартное отклонение, тем выше риск доходности активов.
Корреляция
Статистический показатель, который показывает, насколько финансовые инструменты схожи между собой. Если рост стоимости одного актива приводит к увеличению в цене другого финансового инструмента, то коэффициент корреляции положительный, что говорит о тесной взаимосвязи, и наоборот. Однако когда изменение стоимости одной ценной бумаги никак не влияет на цену другой, то корреляция в таком случае стремится к нулю.
Бета
Коэффициент, который показывает, как ведет себя отдельный финансовый инструмент относительно всего фондового рынка.
Значение коэффициента:
- Бета более 1. Актив очень волатилен, но изменение его стоимости идентично фондовому рынку.
- Ровно 1. Ценная бумага всегда движется в одну сторону, что и рынок, и их волатильность одинакова.
- От 0 до 1. Финансовый инструмент и рынок двигаются в одну сторону, но процентное изменение доходности актива меньше.
- От −1 до 0. Движение актива и фондового рынка направлено в противоположные стороны. Финансовый инструмент в таком случае более стабилен.
- Бета менее −1. Ценная бумага и рынок движутся разнонаправленно. Финансовый актив более волатилен по сравнению с рынком.
Коэффициент Шарпа
Данный коэффициент дает четкое понимание того, как разумно формировать свой портфель. Чтобы определить значение коэффициента, необходимо воспользоваться следующей формулой:
(Доходность портфеля – Безрисковая процентная ставка / Стандартное отклонение)
В качестве безрисковой процентной ставки стоит использовать процентную ставку по правительственным облигациям. Чем выше значение коэффициента Шарпа, тем эффективнее инвестиционная стратегия.
Значение коэффициента Шарпа
Пример расчета
В портфеле имеются две акции: Сбербанка и ВТБ.
Цель: рассчитать коэффициент Шарпа для каждой акции и выяснить, принесет ли данный актив в будущем прибыль для инвестора.
Рассматриваемый период – 365 дней.
Собираем данные:
Годовая доходность акции Сбербанка за прошлый год составила 10%, ВТБ – 4%.
Безрисковым активом будет считаться облигация федерального займа (ОФЗ) с годовой доходностью 7%.
Теперь рассчитаем среднедневную доходность каждого актива по формуле:
(Годовая доходность, % / 365)
Получаем:
Среднедневная доходность ОФЗ равна 0.019%.
Среднедневная доходность акции Сбербанка равна 0.027%.
Среднедневная доходность акции ВТБ равна 0.011%.
Рассчитываем стандартное отклонение:
Стандартное отклонение по компании рассчитывается в excel по формуле =СТАНДОТКЛОН (), где в диапазон берется доходность актива за каждый рассматриваемый нами торговый день (в нашем примере – 365 дней).
Стандарт. отклонение по акции Сбербанка равно 0.09.
Стандарт. отклонение по акции ВТБ равно 0.03.
Примечание! Торги по акциям проводятся не все 365 дней, а гораздо меньше. 365 дней в нашем случае – это условная цифра.
Рассчитываем коэффициент Шарпа:
Коэффициент Шарпа по акции Сбербанка:
(0.027 – 0.019) / 0.09 = 0.08
Коэффициент Шарпа по акции ВТБ:
(0.011 – 0.019) / 0.03 = −0,26
Подводим итог:
Коэффициент Шарпа по акции Сбербанка равен 0.08. Это означает, что актив не высокодоходный. Рисков нет, но и доходность будет крайне мала. В данном случае акции Сбербанка подходят только для формирования умеренного портфеля.
Коэффициент Шарпа по акции ВТБ равен −0.26. Данный актив не рекомендуется включать даже в состав умеренного портфеля, так как акция, скорее всего, не принесет никакого дохода в будущем году и окажется убыточным активом.
Как рассчитывается
Формула расчета выглядит непростой для понимания:
КШ = МО (Д – Да) / СО, где:
Д — доходность анализируемого инструмента или портфеля;
Да — базовая доходность альтернативного инструмента, в качестве которого обычно используется финансовый актив с минимальным риском (государственные облигации или страхуемые депозиты);
МО — математическое ожидание;
СО — стандартное отклонение доходности актива от базовой.
Сложно? Разберем подробнее.
Разницу между нормой прибыли анализируемого и базового финансового инструмента часто называют «премией за риск» — дополнительные деньги, получаемые инвестором за более рискованные вложения.
Математическое ожидание есть не что иное, как среднее значение отклонений волатильной величины, в нашем случае, рентабельности выбранного актива от базовой за рассматриваемый период. В самом простом случае дискретного равномерного распределения (по дням, неделям, месяцам) это — обычное среднее арифметическое всех отклонений:
МО = ∑ Д / N — ∑ Да / N, где N — количество периодов.
Другими словами, это просто разница между средней нормой прибыли анализируемого и базового актива.
Пример 1. Цена акций в течение года в среднем увеличивалась на 3% в месяц. Государственные облигации за этот же период сгенерировали 1% в месяц. Математическое ожидание равно 2%.
С числителем разобрались. Стандартное отклонение в знаменателе отражает степень волатильности, то есть показывает, насколько сильно изменяется доходность (или ее отклонение от базовой величины) от периода к периоду. Зачем вообще это знать? Приведем простой пример.
Пример 2. Акции три года планомерно росли в цене: 20, 25, 30%. Не трудно подсчитать арифметическое среднее: 25%. Стоимость бумаг менялась следующим образом: 40, -20, 55%. Средняя величина: 25%. Ну, и куда вы будете инвестировать? Очевидно, в бумаги «Альфа», которые гарантируют устойчивый, стабильный рост. Ценовые взлеты «Бета» чередуются с падениями, а, значит, получение прибыли не гарантировано (повышенные риски).
Стандартное отклонение говорит именно о величине разброса прибылей и убытков. Чем оно больше, тем рисковее вложения. С математической точки зрения, рассчитывается по формуле:
СО= √(∑(П — Пср)^2/(N-1))
П — премия за риск за короткий временной отрезок в пределах анализируемого периода;
Пср — средняя арифметическая премия за риск;
N — количество временных отрезков.
Не волнуйтесь, для расчета стандартного отклонения даже в Excel есть простая формула СТАНДОТКЛОН. Очевидно также, что, если в качестве базовой рентабельности вы используете постоянную величину, стандартное отклонение можно рассчитывать прямо по выборке доходности, а не премии за риск.
Разобравшись со всеми теоретическими аспектами калькуляции, перейдем к практике.
Пример 3. В таблице показан пример расчета для акций ПАО Сбербанк за 2021 год.
| Месяц | Дата | Цена закрытия (руб). | Прибыль за месяц | Доходность индекса гос. бумаг | Премия за риск |
| 1 | 29.01.2016 | 96,50 | -1,5% | 1,2% | -2,8% |
| 2 | 29.02.2016 | 107,00 | 10,9% | 1,2% | 9,6% |
| 3 | 31.03.2016 | 109,90 | 2,7% | 1,2% | 1,5% |
| 4 | 29.04.2016 | 123,55 | 12,4% | 1,2% | 11,2% |
| 5 | 31.05.2016 | 132,56 | 7,3% | 1,2% | 6,1% |
| 6 | 30.06.2016 | 133,00 | 0,3% | 1,2% | -0,9% |
| 7 | 29.07.2016 | 139,15 | 4,6% | 1,2% | 3,4% |
| 8 | 31.08.2016 | 143,50 | 3,1% | 1,2% | 1,9% |
| 9 | 30.09.2016 | 145,34 | 1,3% | 1,2% | 0,0% |
| 10 | 31.10.2016 | 147,40 | 1,4% | 1,2% | 0,2% |
| 11 | 30.11.2016 | 158,70 | 7,7% | 1,2% | 6,4% |
| 12 | 30.12.2016 | 173,25 | 9,2% | 1,2% | 7,9% |
| Среднее значение: | 4,9% | 1,2% | 3,7% | ||
| Стандартное отклонение: | 4,5% | ||||
| К. Шарпа: | 0,83 |
Допущения:
Близкий к единице коэффициент Шарпа показывает великолепные результаты за 2021 год, даже учитывая, что в качестве альтернативной ставки был использован повышенный индекс. Остается только выбрать альтернативный объект вложений, провести его анализ и сравнить параметры. Но с этим вы справитесь сами.
Предостережения относительно использования коэффициента Шарпа.
Коэффициент Шарпа является основой оценки эффективности финансовых активов. Но необходимо сделать два предостережения относительно его использования: одно связано с интерпретацией отрицательных коэффициентов Шарпа, а другое — с концептуальными ограничениями.
Финансовая теория говорит нам, что в долгосрочной перспективе инвесторам следует компенсировать дополнительную среднюю доходность сверх безрисковой ставки для принятия дополнительного риска, по крайней мере, если рискованный портфель хорошо диверсифицирован. Если инвесторы получат такую компенсацию, числитель коэффициента Шарпа будет положительным.
Тем не менее, мы часто обнаруживаем, что портфели демонстрируют отрицательные коэффициенты Шарпа, когда соотношение рассчитывается за периоды, в которых доминируют медвежьи рынки акций
Это повышает осторожность при работе с отрицательными коэффициентами Шарпа
При работе положительными коэффициентами Шарпа, коэффициент Шарпа для портфеля уменьшается, если мы увеличиваем риск, при прочих равных условиях.
Этот результат является интуитивно понятным для оценки эффективности с поправкой на риск. Однако при отрицательных коэффициентах Шарпа увеличение риска приводит к увеличению коэффициента Шарпа в цифровом выражении (например, удвоение риска может увеличить коэффициент Шарпа с -1 до -0,5).
Поэтому, сравнивая портфели с отрицательными коэффициентами Шарпа, мы обычно не можем считать, что больший коэффициент Шарпа (тот, который ближе к нулю) означает лучшую эффективность с поправкой на риск.
Однако, если стандартные отклонения равны, портфель с отрицательным коэффициентом Шарпа, близким к нулю, имеет преимущество.
На практике, чтобы сделать интерпретируемое сравнение с использованием коэффициента Шарпа, нам может потребоваться увеличить период оценки так, чтобы один или несколько коэффициентов Шарпа стали положительными. Финансовый аналитик также может рассмотреть возможность использования другого показателя для оценки эффективности.
Концептуальное ограничение коэффициента Шарпа состоит в том, что он учитывает только один аспект риска — стандартное отклонение доходности. Стандартное отклонение является наиболее подходящим показателем риска для портфельных стратегий с приблизительно симметричным распределением доходности. Стратегии с опционными элементами имеют асимметричную доходность.
Соответственно, инвестиционная стратегия может приносить частые небольшие выгоды, но потенциально может привести к нечастым, но чрезвычайно большим убыткам. Это утверждение описывает обратное распределение с отрицательной асимметрией. Мы обсудим асимметрию позже.
Такая стратегия иногда образно описывается как «собирание монет перед бульдозером». Например, некоторые стратегии хедж-фондов имеют тенденцию к подобной модели доходности.
Рассчитанный за период, в течение которого работает стратегия (т.е. больших убытков не произошло), этот тип стратегии будет иметь высокий коэффициент Шарпа. В этом случае коэффициент Шарпа дал бы слишком оптимистичную картину показателей, скорректированных с учетом риска, поскольку стандартное отклонение не полностью измеряет принимаемый инвесторами риск.
Поэтому, прежде чем применять коэффициент Шарпа для оценки работы менеджера, мы должны оценить, адекватно ли описывает стандартное отклонение риск инвестиционной стратегии менеджера.
Приведенный ниже пример иллюстрирует вычисление коэффициента Шарпа в контексте оценки эффективности портфеля.
Коэффициент Шарпа
Коэффициент Шарпа, как и альфа, оценивает труд управляющего. Только сравнивает доходность портфеля не с движением какого-либо эталона, а с колебанием доходности самого портфеля за анализируемый период. Т.е. дается «внутренняя» оценка «качества» доходности портфеля, без использования «внешних» данных. Другими словами, дается абсолютная, а не относительная оценка полученной за период доходности.
• R — доходность портфеля (актива)
• Rf — доходность от альтернативного вложения
• σ — стандартное отклонение доходности портфеля (актива)
Колебания доходности — это риск. Высокие колебания — это высокий риск, и они должны приносить высокий доход. Колебания доходности измеряются стандартным отклонением, которое помещается в знаменатель дроби, рассчитывающей коэффициент Шарпа. В числителе дроби – доходность портфеля, очищенная от гарантированной рыночной доходности — от доходности безрискового вложения, в качестве которого, как правило, берется депозит в Сбербанке.
Если портфель показал доходность 30% со стандартным отклонением равным 10, а депозит Сбербанка принес бы 12%, то коэффициент Шарпа будет равен (30-12)/10 = 1,8. Можно сказать, что за каждую единицу риска были получены 1,8 единиц доходности сверх гарантированной безрисковой доходности.
Чем значение коэффициента Шарпа выше, тем выгоднее управляющий использует риск портфеля. Причем, благодаря тому, что этот коэффициент использует стандартное отклонение доходности самого портфеля, а не внешний эталон, он может быть применен для сравнения между собой различный портфелей.
При одинаковой доходности портфели могут иметь разные значения этого коэффициента, потому что они принимают на себя разное количество риска. Портфель, у которого коэффициент Шарпа выше при одинаковой доходности, достиг результата с меньшим риском. Чем выше стандартное отклонение, тем больше знаменатель уравнения коэффициента Шарпа, а значит портфелю нужно показывать высокую доходность, чтобы заработать высокое значение этого показателя. Портфелю с низким уровнем риска (небольшим стандартным отклонением) достаточно показывать умеренную доходность, чтобы его коэффициент Шарпа был достаточно высоким.
У коэффициента Шарпа есть преимущество перед альфой. Стандартное отклонение измеряет волатильность фонда в абсолютной величине, а не относительной, как альфа. Поэтому, если для полезности альфы должен быть высоким коэффициент корреляции, то коэффициент Шарпа всегда имеет полноценное значение, независимо от других показателей.
Вывод

В большинстве случаев, коэффициент Шарпа покажет реальную рентабельность стратегии. Но, иногда, показатель Шарпа может вводить в заблуждение. Например, некоторые облигации могут показывать стабильную доходность выше банковского процента в течении многих лет, на что коэффициент ответит нереалистично высокими показателями. В этом случае, полученное значение ничего не скажет о реальных рисках, стоящих за инвестированием в данную облигацию, пусть даже риск будет на самом деле минимальным. В целом же, данный коэффициент подойдёт для сравнения двух стратегий с относительно частыми входами и не самыми огромными целями.


























